Given the previous posts on magnetic recording, we are now in the position to look at unconventional magnetic recording. In other words, instead of applying a write field of sufficient strength to switch magnetic grains, we look at other ways to switch a magnetic grain. This has become to be known as “energy assist magnetic recording”. In future recording systems this will be required since there is a limit on the applied field one can produce in a small area.
Heat assisted magnetic recording (HAMR) is one approach. There are excellent reviews in the literature (and many questionable papers). However the common misconception about HAMR is energy requirements and high temperatures. Yes, during writing, four or five magnetic grains are at ~700K ~ 425C ~ 800F, for about 1ns. The volume of these grains are ~500nm![]() currently and will become smaller. Magnetic grains are metallic and a simple calculation shows amount of energy required is measured in pico-Joules. The concern is across the “air gap”: the recording head. A near field transducer (NFT) has plasmons excited by an external laser which evanescently couples across the air gap to the magnetic grains. The driven plasmons will result in resistive losses in the NFT. Since the ideal material for NFTs are noble metals (i.e. Drude-like permeabilities), even small elevations in temperature can deform/melt the NFT. Identifying a material that gives both performance and reliability is a continuing effort.
currently and will become smaller. Magnetic grains are metallic and a simple calculation shows amount of energy required is measured in pico-Joules. The concern is across the “air gap”: the recording head. A near field transducer (NFT) has plasmons excited by an external laser which evanescently couples across the air gap to the magnetic grains. The driven plasmons will result in resistive losses in the NFT. Since the ideal material for NFTs are noble metals (i.e. Drude-like permeabilities), even small elevations in temperature can deform/melt the NFT. Identifying a material that gives both performance and reliability is a continuing effort.
Microwave assisted magnetic recording (MAMR) is another approach. Here, a time varying applied field resonantly pumps energy into a magnetic moment until it has enough to over come the energy barrier and switch orientations (if that was confusing, perhaps start here). Most implementations of MAMR use a time varying applied field that is either circular or linear in the plane of the magnetic medium. Typically, a spin torque oscillator (STO) is used to generate this microwave magnetic field. Magnitude and direction of electrical current through the STO affects frequency and chirality of the fields while orientation and geometry of STO affects chirality, polarization and strength including out-of-plane fields. A comprehensive model of electric current, STO, magnetic write head and magnetic storage medium is a challenging (but doable) computational problem.
We will simplify by limiting ourselves to the ‘best case’. The write field from the magnetic head is described, once again, by ![]() uniform in space. The microwave field will be in-plane, circular polarized and also uniform in space,
uniform in space. The microwave field will be in-plane, circular polarized and also uniform in space, ![]() where
where ![]() and
and ![]() are either constants or linear in time. We start from equilibrium and ramp
are either constants or linear in time. We start from equilibrium and ramp ![]() (
(![]() ) from 0 to
) from 0 to ![]() (
(![]() ) in 0.1ns, hold constant for a further 0.4ns and then ramped back down to 0 in 0.1ns (typical write condition). We sweep
) in 0.1ns, hold constant for a further 0.4ns and then ramped back down to 0 in 0.1ns (typical write condition). We sweep ![]() from 0.5 to 2.5kOe in steps of 0.1kOe and
from 0.5 to 2.5kOe in steps of 0.1kOe and ![]() from 20 to 60GHz in 1GHz steps to generate a contour of the probability of a grain switching.
from 20 to 60GHz in 1GHz steps to generate a contour of the probability of a grain switching.
We start with 481 extruded (10nm) grains with mean diameter of 8nm and a standard deviation of 0.4nm at 83% packing fraction. Each grain has identical material parameters: ![]() kOe,
kOe, ![]() (
(![]() ) is normal to media plane,
) is normal to media plane, ![]() emu/cc and
emu/cc and ![]() .
.
We first look at isolated grains. Here, convention writing (i.e. ![]() ) requires
) requires ![]() kOe for
kOe for ![]() K for 100% switching.
K for 100% switching.
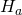 (kOe) and
(kOe) and 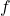 (GHz) for
(GHz) for 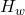 =10kOe. Left at temperature 0K and right at 318K.
=10kOe. Left at temperature 0K and right at 318K.We will assume there are nine magnetic grains in a bit and to successfully write we need to switch at least eight magnetic orientations. Since the grains are independent (isolated), ![]() (red) contours are at least 99% certain at least 8 of 9 grains will be switched,
(red) contours are at least 99% certain at least 8 of 9 grains will be switched, ![]() (orange) are at least 90% (80%) certain while
(orange) are at least 90% (80%) certain while ![]() (green and below) at least 50% certain 7 or less grains will be switched. Thermal effects (i.e.
(green and below) at least 50% certain 7 or less grains will be switched. Thermal effects (i.e. ![]() ) smooth and extend the contour, Fig 1. For isolated grains, there is a large phase space for
) smooth and extend the contour, Fig 1. For isolated grains, there is a large phase space for ![]() and
and ![]() to achieve sufficient probability of switching.
to achieve sufficient probability of switching.
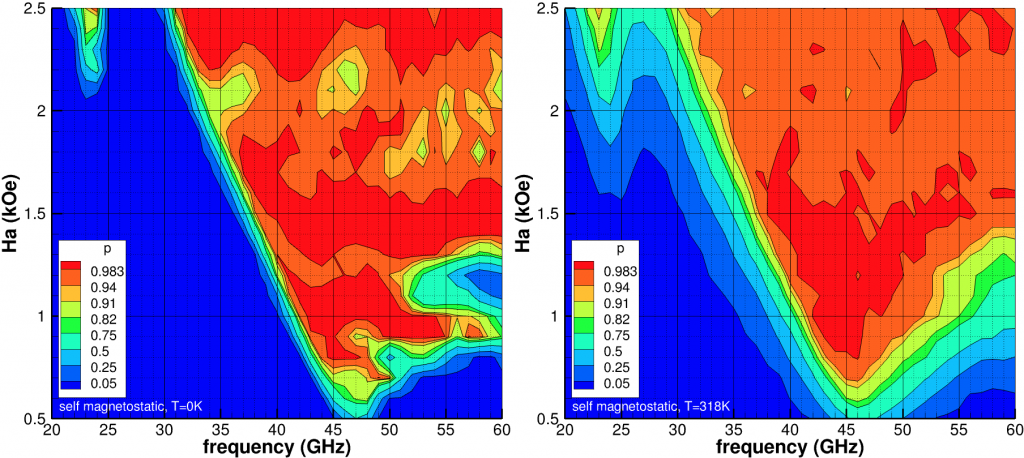
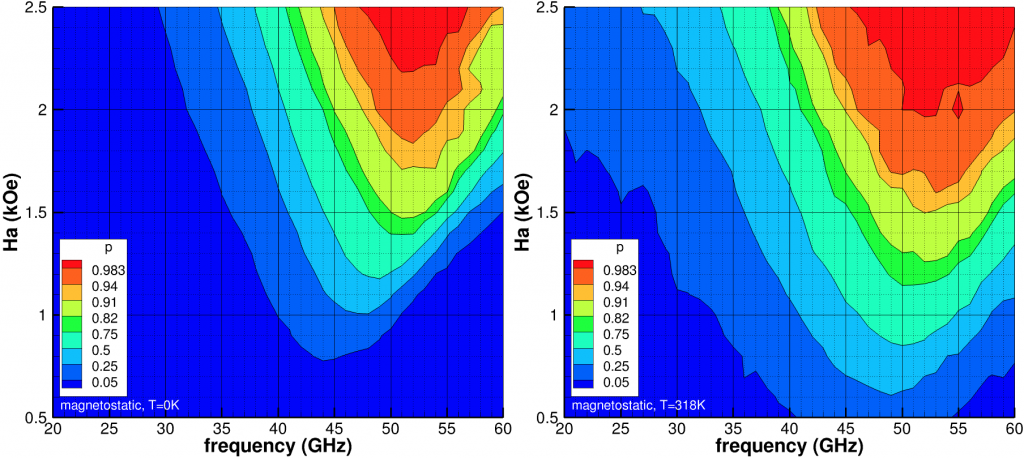
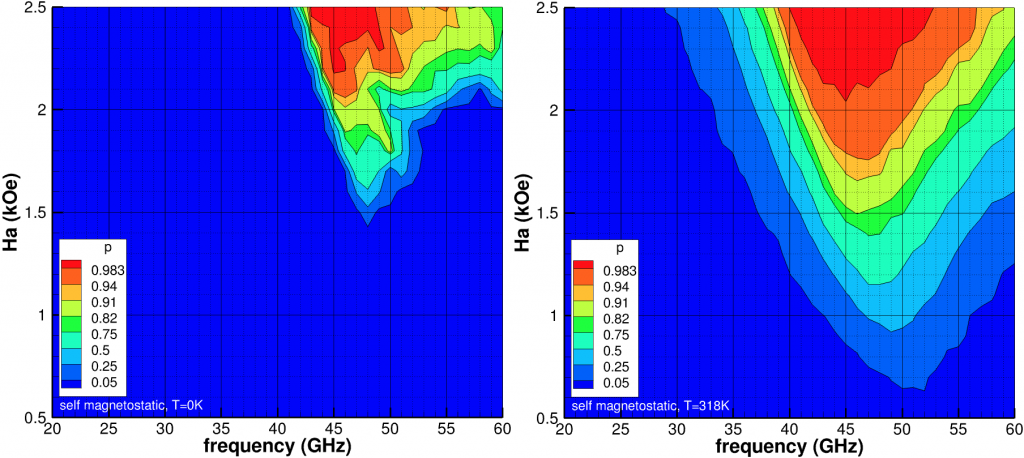
Looking at a collection of grains (Fig. 2), we start with randomly assigning up or down magnetic orientations and then compute the probability the up orientation will be written (the down orientation is not affected by ![]() due to incorrect chirality). We then reset to the random orientation, switch the chirality of
due to incorrect chirality). We then reset to the random orientation, switch the chirality of ![]() , the sign of
, the sign of ![]() and compute the probability of the down orientation will be written. We plot the weighted averaged of these probabilities:
and compute the probability of the down orientation will be written. We plot the weighted averaged of these probabilities:
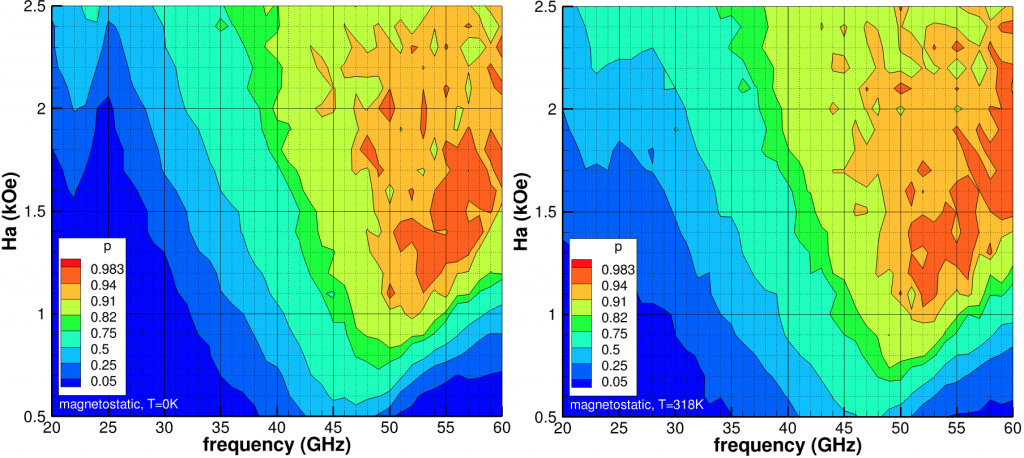
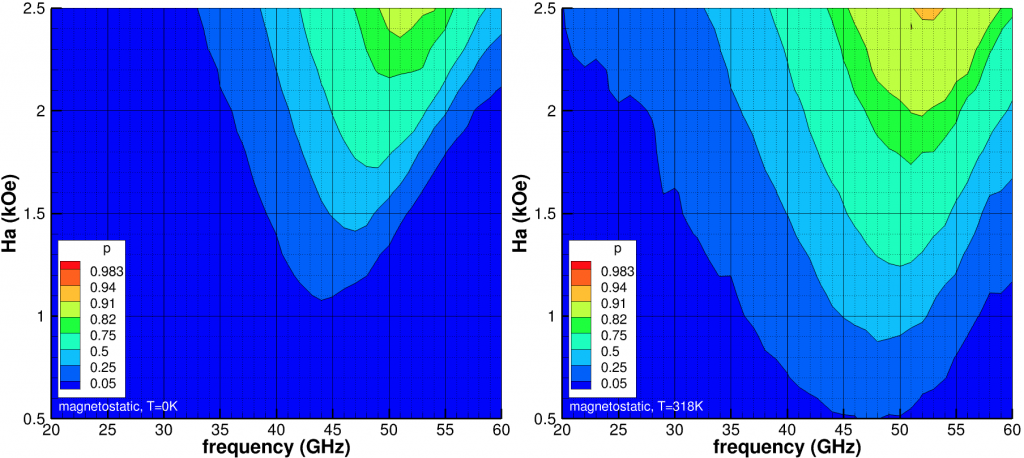
 (kOe) and
(kOe) and  (GHz) for
(GHz) for  =10kOe. Left at temperature 0K and right at 318K. Initial condition is AC magnetization.
=10kOe. Left at temperature 0K and right at 318K. Initial condition is AC magnetization.Including the full magnetostatic field (Fig. 2), the probability of switching reduces overall while the optimal frequency and ![]() both increase. The shift in frequency is partially explained by the magnetostatic field when the medium sample approaches saturation. Regardless, the viable phase space has shrunk while the peak probabilities have also decreased. For completeness, we note
both increase. The shift in frequency is partially explained by the magnetostatic field when the medium sample approaches saturation. Regardless, the viable phase space has shrunk while the peak probabilities have also decreased. For completeness, we note ![]() kOe is sufficient for conventional write, i.e.
kOe is sufficient for conventional write, i.e. ![]() , for
, for ![]() K for 100% switching.
K for 100% switching.
Current magnetic grains are actually segmented: instead of one uniform magnetic orientation, five or more magnetic orientations are stacked vertically with the same lateral dimensions but different thicknesses and material properties [1]. We follow [1] using the same lateral microstructure as above, ![]() emu/cc for each layer with nominal
emu/cc for each layer with nominal ![]() kOe. However, Table 1 shows that such 5 layer grains can be written when
kOe. However, Table 1 shows that such 5 layer grains can be written when ![]() kOe except for isolated grains at
kOe except for isolated grains at ![]() K. To avoid this problem, we use a nominal
K. To avoid this problem, we use a nominal ![]() kOe.
kOe.
| grain ensemble | number of layers | initial orientation | nominal | [ | [ | [ |
| isolated | 1 | any | 28 | 14.1 [11.9] | 14.7 [14.3] | 0.6 [2.4] |
| collection | 1 | up | 28 | 9.8 [7.6] | 16.8 [16.4] | 7.0 [8.8] |
| collection | 1 | random | 28 | 11.7 [10.7] | 16.8 [16.6] | 5.1 [5.9] |
| isolated | 5 | any | 28 | 10.7 [6.8] | 11.1 [10.3] | 0.4 [3.5] |
| collection | 5 | up | 28 | 6.6 [3.4] | 12.9 [12.3] | 6.3 [8.9] |
| collection | 5 | random | 28 | 8.6 [6.2] | 12.9 [12.6] | 4.3 [6.4] |
| isolated | 5 | any | 42 | 15.8 [11.2] | 16.2 [15.3] | 0.4 [4.1] |
| collection | 5 | up | 42 | 11.7 [7.9] | 16.9 [17.5] | 5.2 [9.6] |
| collection | 5 | random | 42 | 13.7 [10.5] | 17.8 [17.4] | 4.1 [6.9] |
Using a 5 layer grain with nominal ![]() kOe and
kOe and ![]() and
and ![]() identical for each layer, we find the probability of isolated 5 layer grain switching:
identical for each layer, we find the probability of isolated 5 layer grain switching:
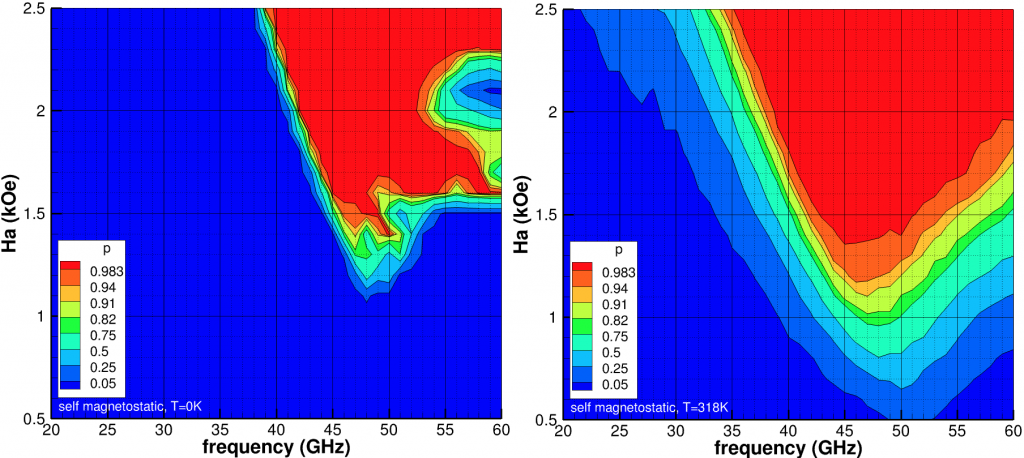
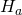 (kOe) and
(kOe) and 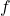 (GHz) for
(GHz) for 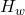 =10kOe. Left at temperature 0K and right at 318K.
=10kOe. Left at temperature 0K and right at 318K.For isolated 5 layer grains (Fig. 3), we see the peak probability of writing is shifted to higher frequency and ![]() compared to a single layer grain (Fig. 1). We also note that the contours appear smoother than a single layer grain. Looking at a collection of grains (Fig. 4), starting from random orientation, otherwise identical, we find
compared to a single layer grain (Fig. 1). We also note that the contours appear smoother than a single layer grain. Looking at a collection of grains (Fig. 4), starting from random orientation, otherwise identical, we find
 (kOe) and
(kOe) and  (GHz) for
(GHz) for  =10kOe. Left at temperature 0K and right at 318K. Initial condition is AC magnetization.
=10kOe. Left at temperature 0K and right at 318K. Initial condition is AC magnetization.While we see the full magnetostatic field (Fig. 4) again shifts the optimal ![]() and
and ![]() to higher values, we see the peak probability actually increases compared to a singe orientation grain (Fig. 2).
to higher values, we see the peak probability actually increases compared to a singe orientation grain (Fig. 2). ![]() once again increases phase space of optimal
once again increases phase space of optimal ![]() and
and ![]() .
.
If ![]() is generated by a localized source (e.g. STO), the field magnitude is expected to decrease with increasing distance from the localized source. Assuming we are sampling the field at distances small compared to the size of the source, the magnitude of
is generated by a localized source (e.g. STO), the field magnitude is expected to decrease with increasing distance from the localized source. Assuming we are sampling the field at distances small compared to the size of the source, the magnitude of ![]() varies as
varies as ![]() where
where ![]() is the distance to the source (i.e. top layer of spins see 100% of
is the distance to the source (i.e. top layer of spins see 100% of ![]() , second layer of spins see 75%, third 60%, fourth 45% and bottom layer 30%). This is roughly the scaling computed from the proposed STO of [1]. Here, isolated 5 layer grain switching probability is found to be:
, second layer of spins see 75%, third 60%, fourth 45% and bottom layer 30%). This is roughly the scaling computed from the proposed STO of [1]. Here, isolated 5 layer grain switching probability is found to be:
 (kOe) in the upper layer of grains and
(kOe) in the upper layer of grains and  (GHz) for
(GHz) for  =10kOe. Left at temperature 0K and right at 318K.
=10kOe. Left at temperature 0K and right at 318K. 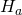 scales as
scales as 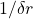 .
.Compared to Fig. 3 (where ![]() was identical for each layer), we need an additional ~0.7kOe to successfully switch the grains. Turning to a collection of grains, initially randomly orientated, we compute the probability of a 5 layer grain to switch:
was identical for each layer), we need an additional ~0.7kOe to successfully switch the grains. Turning to a collection of grains, initially randomly orientated, we compute the probability of a 5 layer grain to switch:
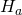 (kOe) in the upper layer of grains and
(kOe) in the upper layer of grains and 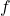 (GHz) for
(GHz) for 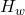 =10kOe. Left at temperature 0K and right at 318K.
=10kOe. Left at temperature 0K and right at 318K. 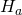 scales as
scales as 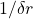 .
.Compared to Fig. 4, we see any ![]() used is not sufficient for high probability of switching.
used is not sufficient for high probability of switching.
This does not say MAMR will not work, but it does illustrate the importance of including finite temperature and a collection of grains since the latter does affect the probability of writing. It appears most modeling uses ![]() K and isolated grain to find the probability of switching and then that distribution is used to construct written bits.
K and isolated grain to find the probability of switching and then that distribution is used to construct written bits.
More detailed simulations would require details of both ![]() and
and ![]() in order to write a data track and neighboring tracks and then a readback to generate a signal which can be fed into a channel model to find the capacity of the recording system. Given the above results and we still need to add distributions of
in order to write a data track and neighboring tracks and then a readback to generate a signal which can be fed into a channel model to find the capacity of the recording system. Given the above results and we still need to add distributions of ![]() ,
, ![]() ,
, ![]() , …, it seems unlikely that such a recording system would perform adequately.
, …, it seems unlikely that such a recording system would perform adequately.

Add a Comment