Theory
In this blog post, we introduce magnetic recording by focusing on the dynamics of writing granular magnetic medium. We start with the Landau-Lifshitz-Gilbert (LLG) equation which is sufficient for describing the dynamics of a grain’s magnetic moment ![]() :
:
![]()
where ![]() is the gyromagnetic constant,
is the gyromagnetic constant, ![]() is the Gilbert damping constant and
is the Gilbert damping constant and ![]() is the ‘effective field‘ found by taking the derivative of the thermodynamic free energy,
is the ‘effective field‘ found by taking the derivative of the thermodynamic free energy, ![]() , with respect to
, with respect to ![]() (i.e.
(i.e. ![]() ). One part of the free energy is the Zeeman energy,
). One part of the free energy is the Zeeman energy, ![]() , where
, where ![]() is an externally applied magnetic field.
is an externally applied magnetic field.
It is easy to show the time rate of change of the thermodynamic free energy to be
![]()
![]()
![]()
where ![]() is the volume of the magnetic grain and
is the volume of the magnetic grain and ![]() was used.
was used.
This equation describes the only way that the free energy of a magnetic moment can change in time according to LLG. The first term on the rhs, ![]() , is simply free energy loss due to Gilbert damping, vanishing when
, is simply free energy loss due to Gilbert damping, vanishing when ![]() . The second term is what we are mostly concerned about. If
. The second term is what we are mostly concerned about. If ![]() is less (greater) than zero then free energy is decreasing (increasing). That is, either the time variation of amplitude
is less (greater) than zero then free energy is decreasing (increasing). That is, either the time variation of amplitude ![]() and/or direction
and/or direction ![]() can affect the free energy. The former tends to change the energy surface (e.g. creating one free energy minima) while the latter can change the free energy of the magnetic moment while not perturbing the energy surface itself (e.g.
can affect the free energy. The former tends to change the energy surface (e.g. creating one free energy minima) while the latter can change the free energy of the magnetic moment while not perturbing the energy surface itself (e.g. ![]() ).
).
Magnetic recording
For a magnetic grain used in magnetic recording, the free energy is
![]()
where ![]() is magnetostatic field,
is magnetostatic field, ![]() is the magnetocrystalline anisotropy (MCA) with ‘easy axis’ along
is the magnetocrystalline anisotropy (MCA) with ‘easy axis’ along ![]() and
and ![]() is exchange energy. Correspondingly,
is exchange energy. Correspondingly,
![]()
Typically inside a grain, ![]() is assumed uniform and
is assumed uniform and ![]() can be ignored (
can be ignored (![]() ). If the isolated grain is in a shape of an ellipsoid, then
). If the isolated grain is in a shape of an ellipsoid, then ![]() is replaced by a modified MCA term:
is replaced by a modified MCA term: ![]() where
where ![]() is the depolarization (or demagnetization) factor along
is the depolarization (or demagnetization) factor along ![]() ranging from
ranging from ![]() (a needle) to
(a needle) to ![]() (pancake) [see]. If not in isolation, other grains would contribute to
(pancake) [see]. If not in isolation, other grains would contribute to ![]() , as a summation of dipole fields in the case of ellipsoidal grains.
, as a summation of dipole fields in the case of ellipsoidal grains.
Regardless, the MCA term determines stable ![]() orientations which
orientations which ![]() must be able to switch between. Without loss of generality, we will write, or switch, a grain starting with
must be able to switch between. Without loss of generality, we will write, or switch, a grain starting with ![]() ~
~ ![]() and going to
and going to ![]() orientation, both being minima of the MCA energy.
orientation, both being minima of the MCA energy.
Conventional write
In typical HDD write, the linear velocity (~20m/s), field rise time (~0.2ns peak-to-peak), write field gradient (~1kOe/nm) and grain size (![]() ~8nm) shows
~8nm) shows ![]() ~100kOe/ns. Even at this rate (Fig. 1 below), the magnetization is in quasi-equilibrium with
~100kOe/ns. Even at this rate (Fig. 1 below), the magnetization is in quasi-equilibrium with ![]() . Without loss of generality, let
. Without loss of generality, let ![]() be normal to the medium plane and align
be normal to the medium plane and align ![]() along
along ![]() then equilibrium
then equilibrium ![]() is given by the minimization of free energy,
is given by the minimization of free energy, ![]() where
where ![]() . For
. For ![]() there is one energy minimum at
there is one energy minimum at ![]() (i.e. successful switch),
(i.e. successful switch), ![]() has two energy minima separated by an energy maximum (incomplete switch), otherwise there can be one or two energy minima depending on the value of
has two energy minima separated by an energy maximum (incomplete switch), otherwise there can be one or two energy minima depending on the value of ![]() (e.g.
(e.g. ![]() has
has ![]() for
for ![]() – the Stoner-Wohlfarth limit).
– the Stoner-Wohlfarth limit).
Dynamic write
Let us consider the alternative ![]() (i.e.
(i.e. ![]() ). Once again, let
). Once again, let ![]() be normal to the medium plane, we can solve LLG directly for the dynamic
be normal to the medium plane, we can solve LLG directly for the dynamic ![]() when we apply an AC in-plane field such that
when we apply an AC in-plane field such that ![]() , say
, say ![]() ,
,
![]()
![]()
such that ![]() (that is, sign of
(that is, sign of ![]() determines if free energy increases or decreases). We see
determines if free energy increases or decreases). We see ![]() switches sign when
switches sign when ![]() passes through ~
passes through ~![]() therefore the flow of free energy also switches sign.
therefore the flow of free energy also switches sign.
The expression for ![]() gives the constraint
gives the constraint ![]() and an analytic time for
and an analytic time for ![]() as
as ![]() .
.
From expression for ![]() , one see the angular frequency of
, one see the angular frequency of ![]() goes as
goes as ![]() . Then average microwave frequency would be
. Then average microwave frequency would be ![]() ~
~![]() GHz/kOe
GHz/kOe ![]() . For
. For ![]() ~ 19.2kOe and we require ~0.1ns to switch then
~ 19.2kOe and we require ~0.1ns to switch then ![]() 600 Oe or ~4 cycles to switch. Larger
600 Oe or ~4 cycles to switch. Larger ![]() could achieve switching with fewer cycles.
could achieve switching with fewer cycles.
Micromagnetic simulations
Detailed micro-magnetic simulations coincide with the analysis for both conventional and dynamic writing. Here we have 1024 identical extruded (10nm) square grains of volume 503nm![]() packed in a periodic square lattice with
packed in a periodic square lattice with ![]() kOe,
kOe, ![]() ,
, ![]() emu/cc and
emu/cc and ![]() . We include the full magnetostatic field
. We include the full magnetostatic field ![]() interactions. However, in the cases below, since the grains, initial condition and applied field histories are identical so are all the spin dynamics. Then
interactions. However, in the cases below, since the grains, initial condition and applied field histories are identical so are all the spin dynamics. Then ![]() , resulting in an effective
, resulting in an effective ![]() . Consider it a test of the underlying numerical routines (all 1024 grains should have identical trajectories even though the numerical procedure does not enforce this unique condition).
. Consider it a test of the underlying numerical routines (all 1024 grains should have identical trajectories even though the numerical procedure does not enforce this unique condition).
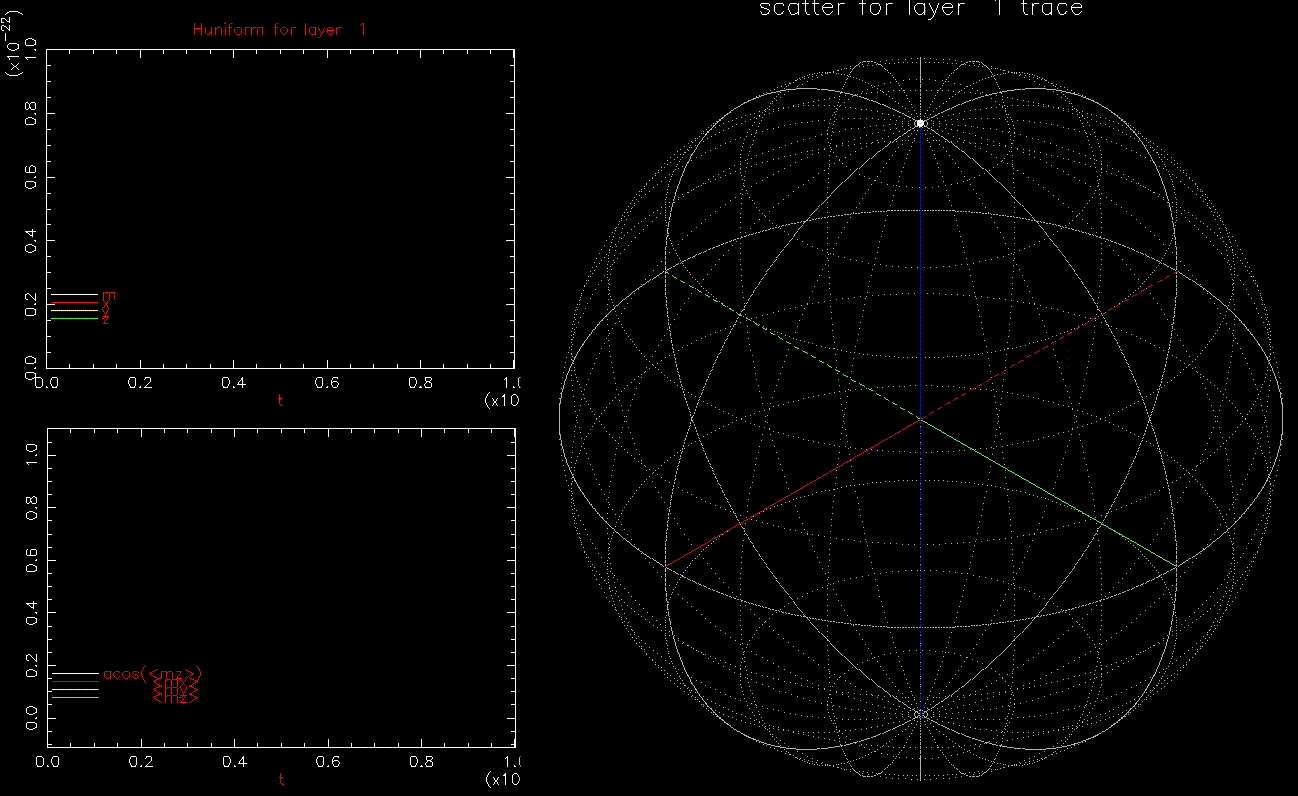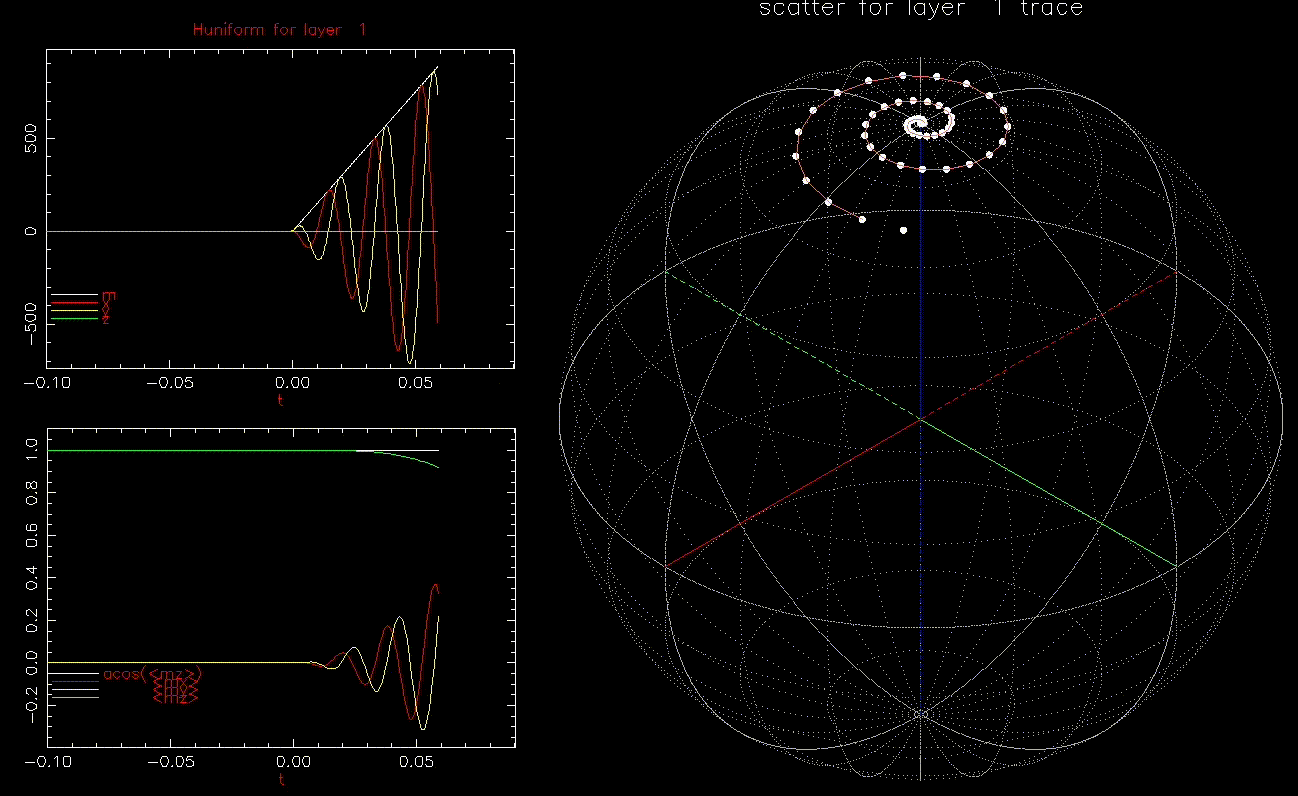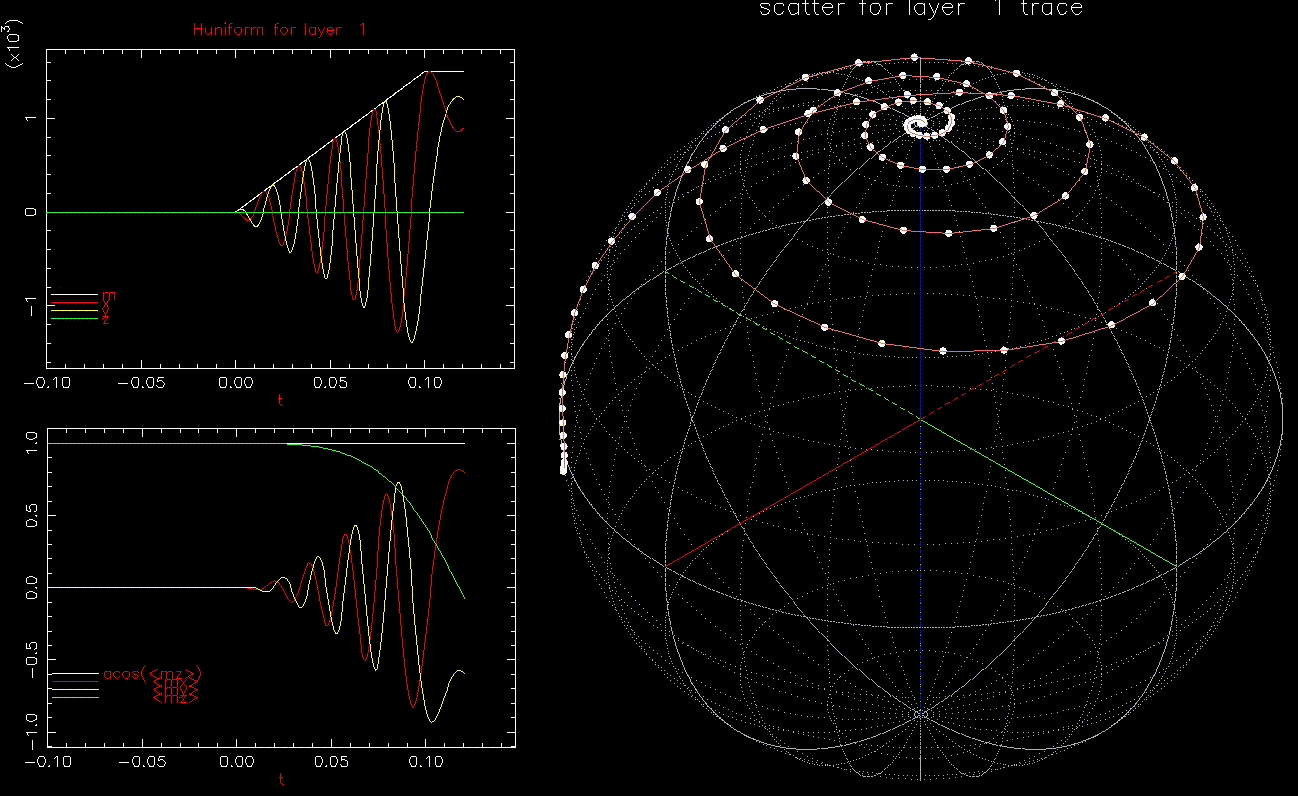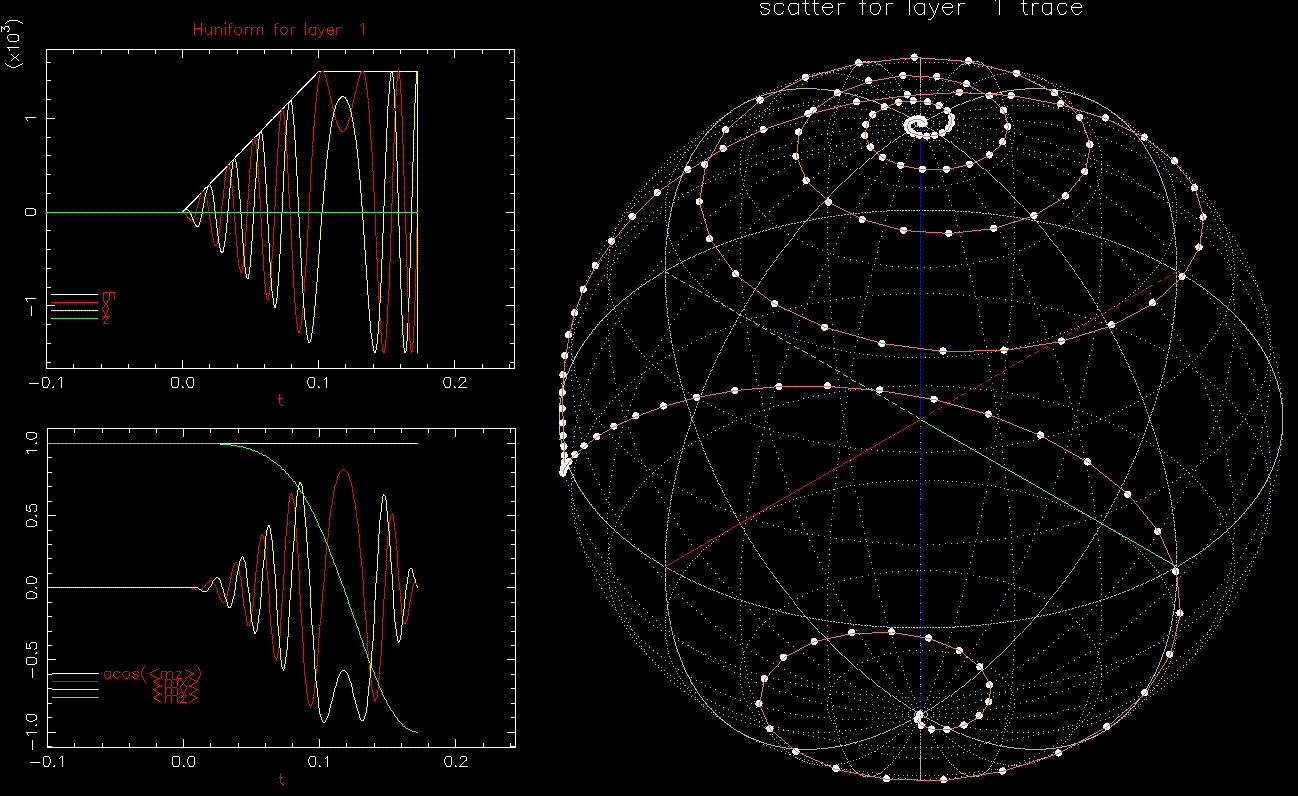
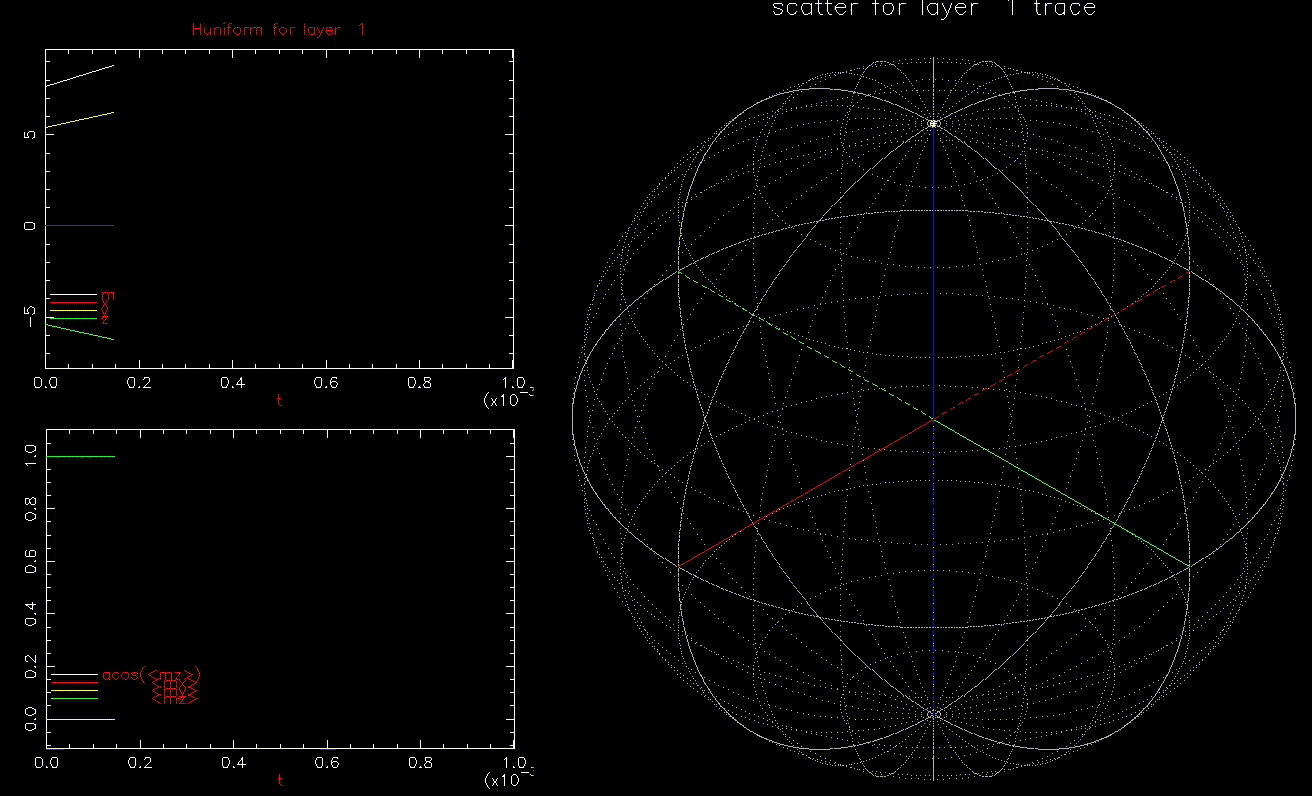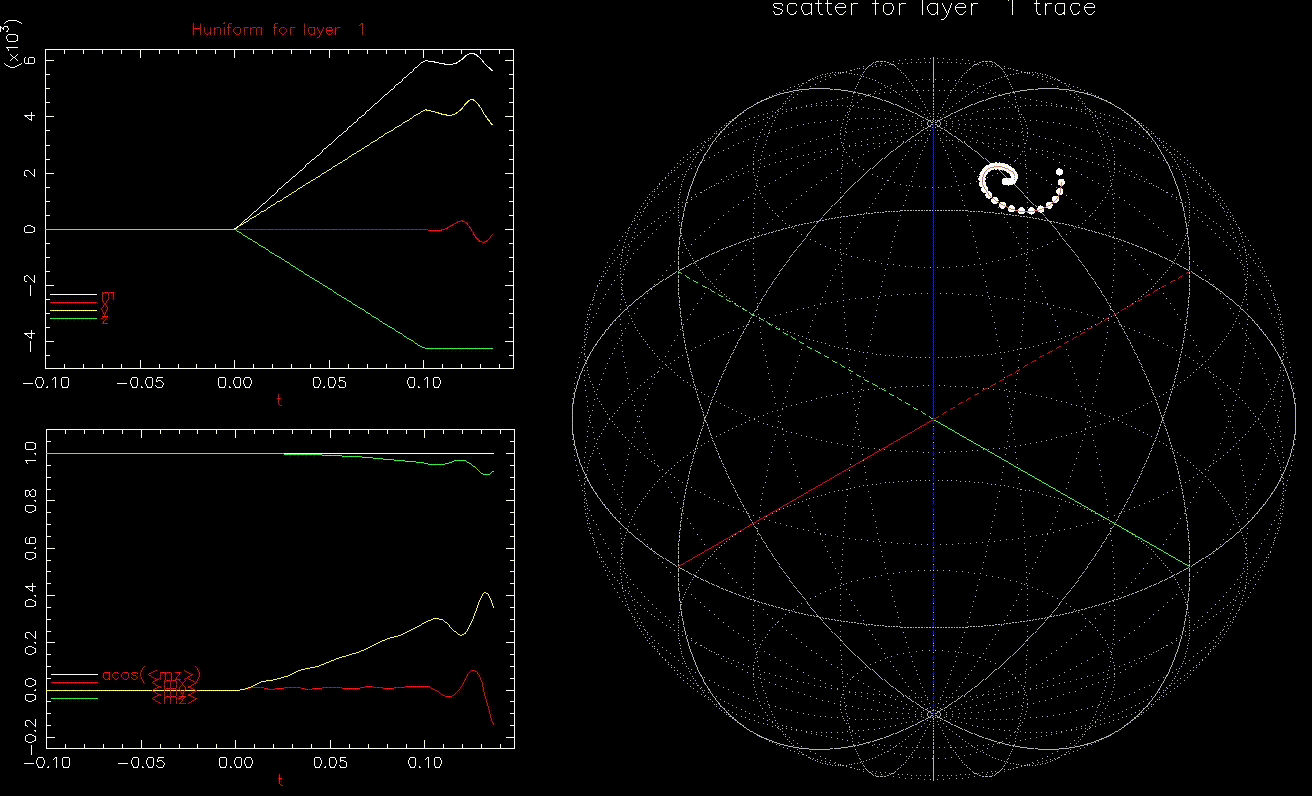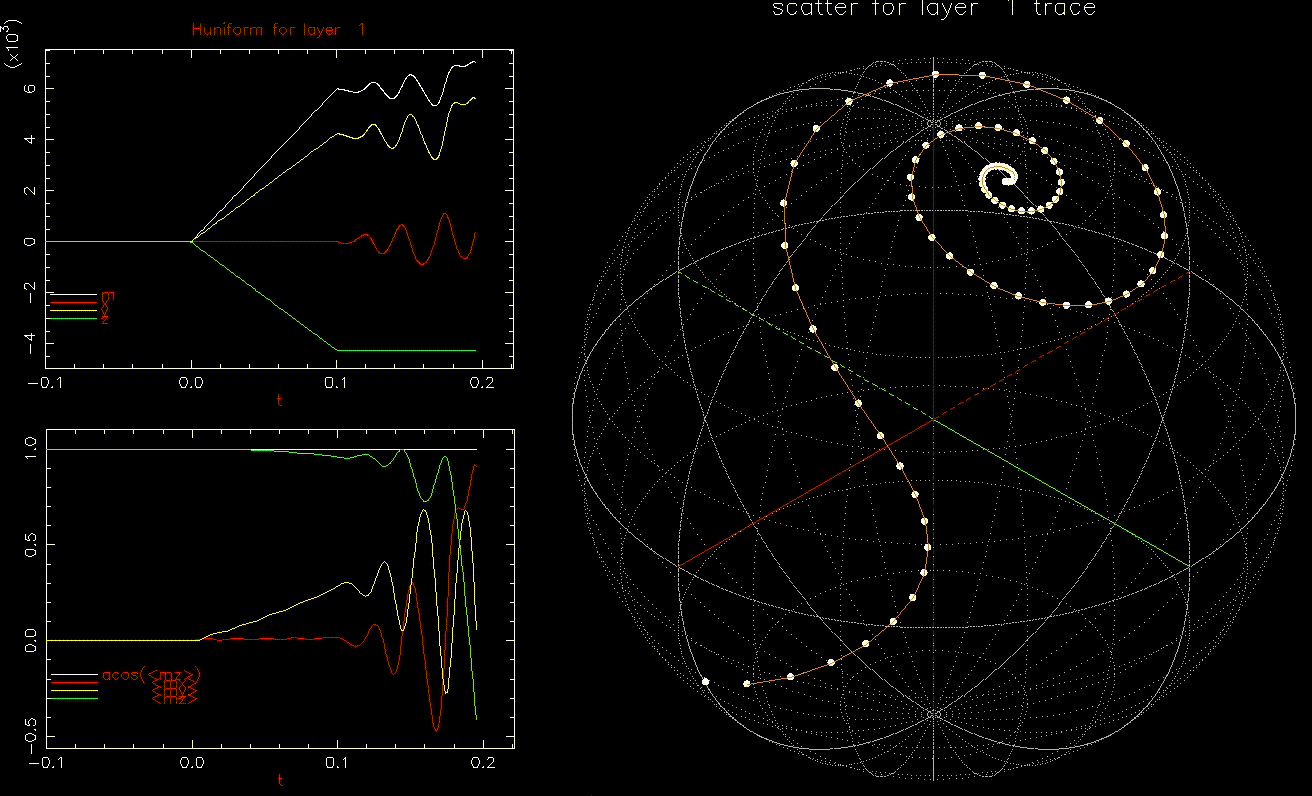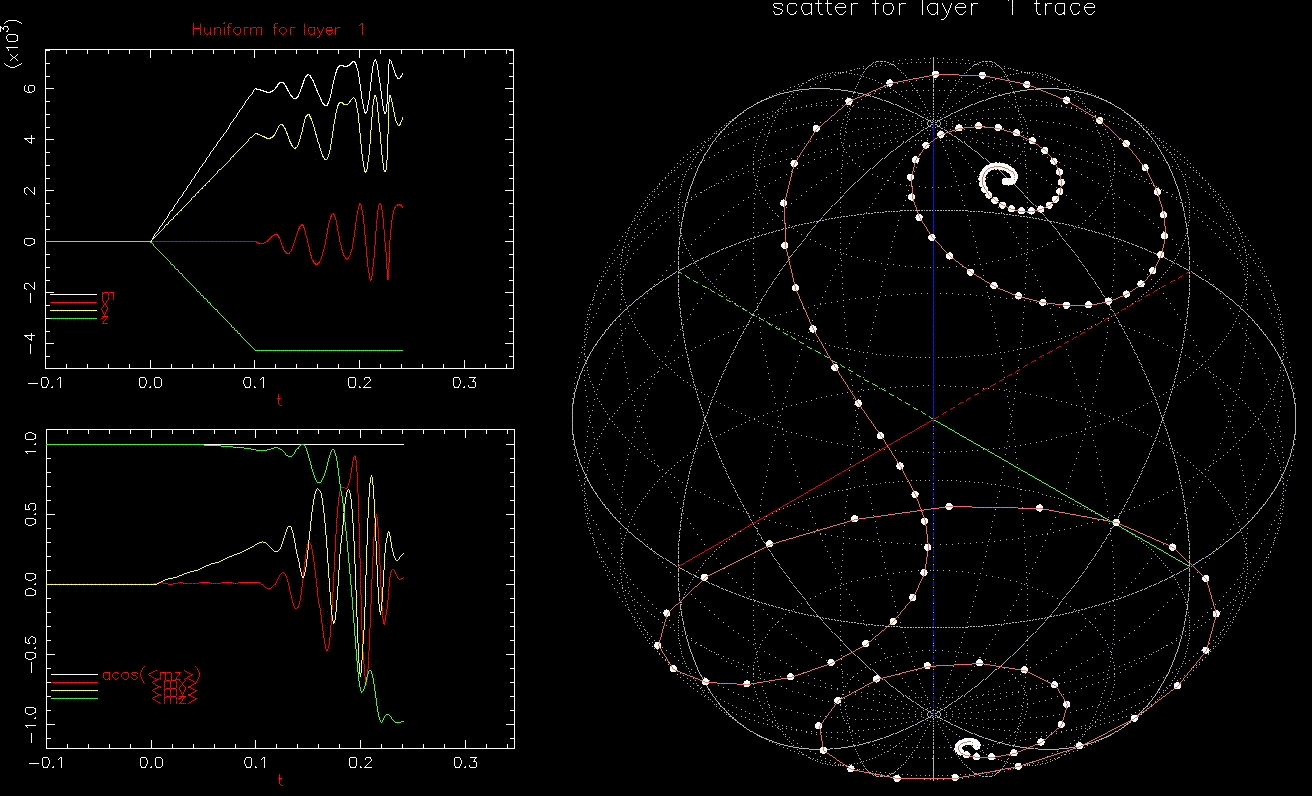
We first do conventional writing by ![]() where
where ![]() is linearly increasing from zero to 10kOe (
is linearly increasing from zero to 10kOe (![]() 9.6kOe) in 0.1ns:
9.6kOe) in 0.1ns:
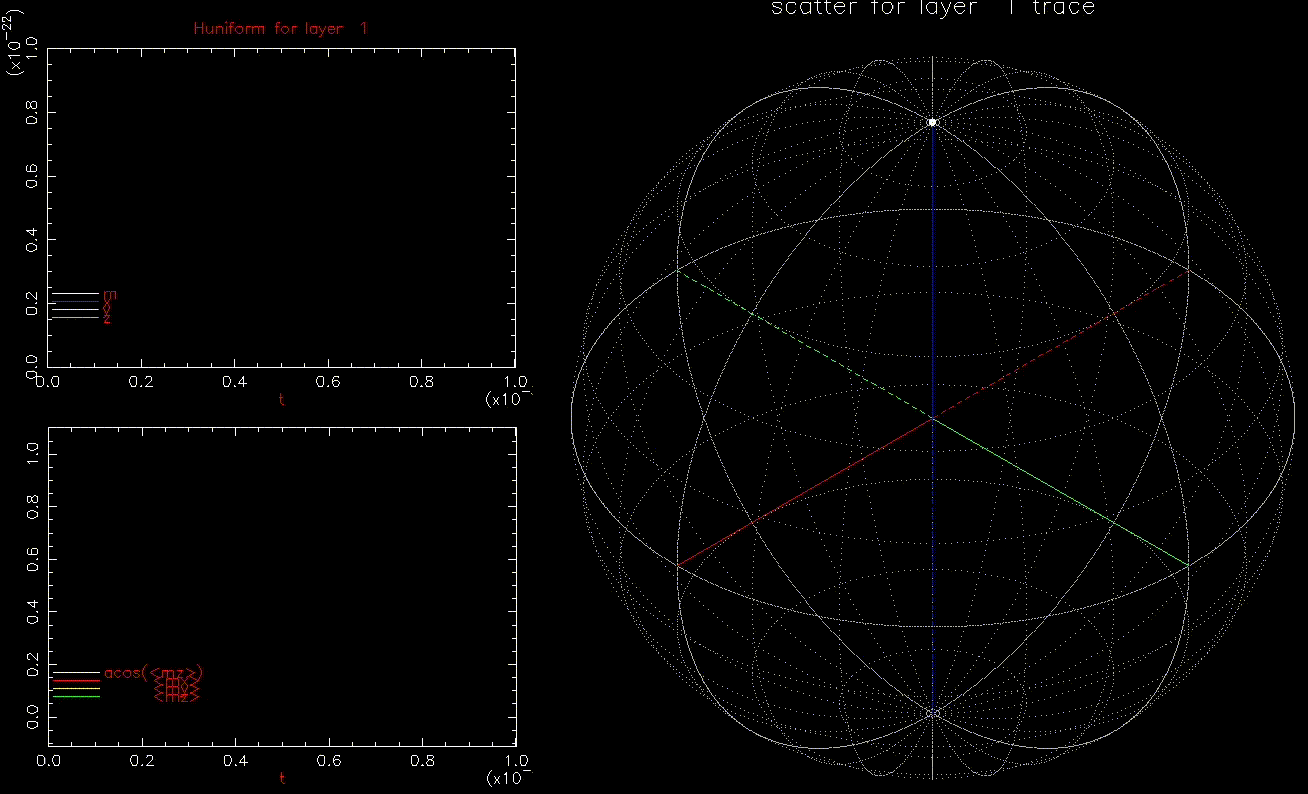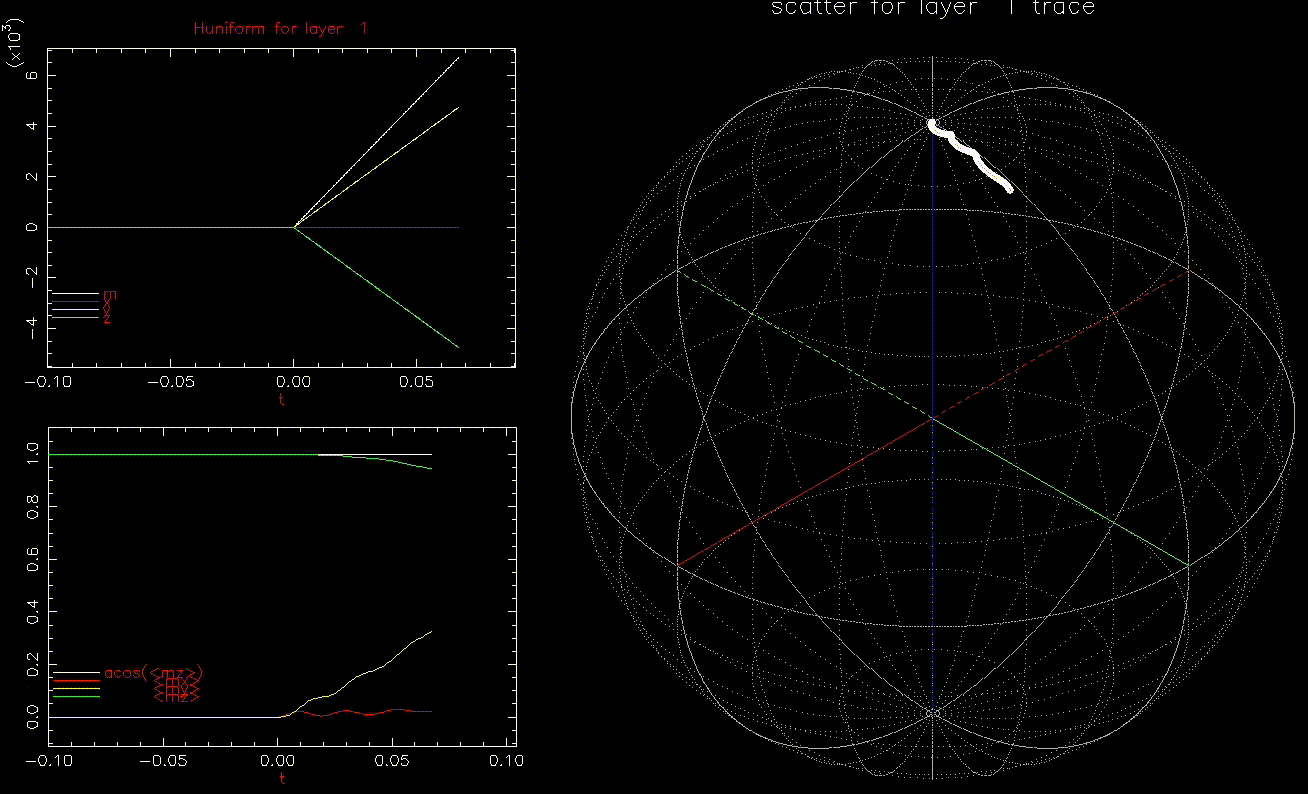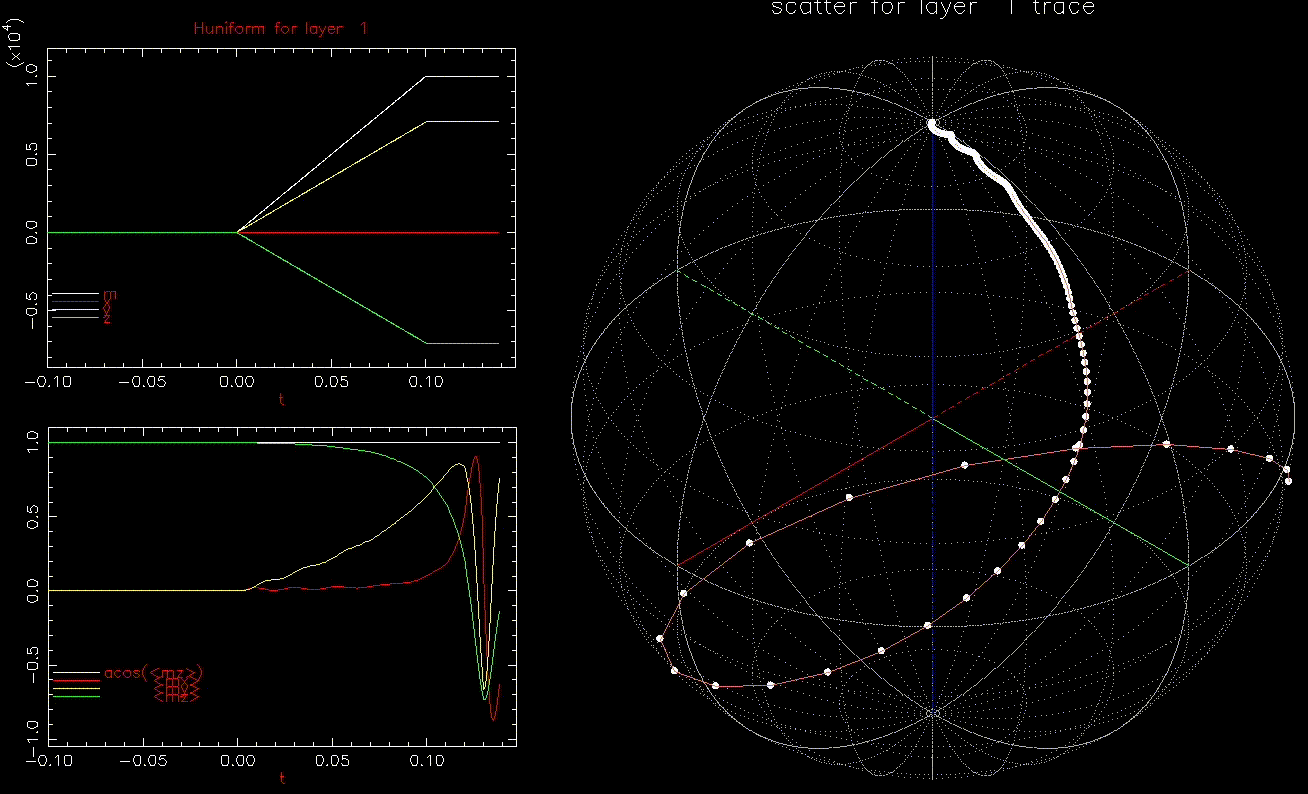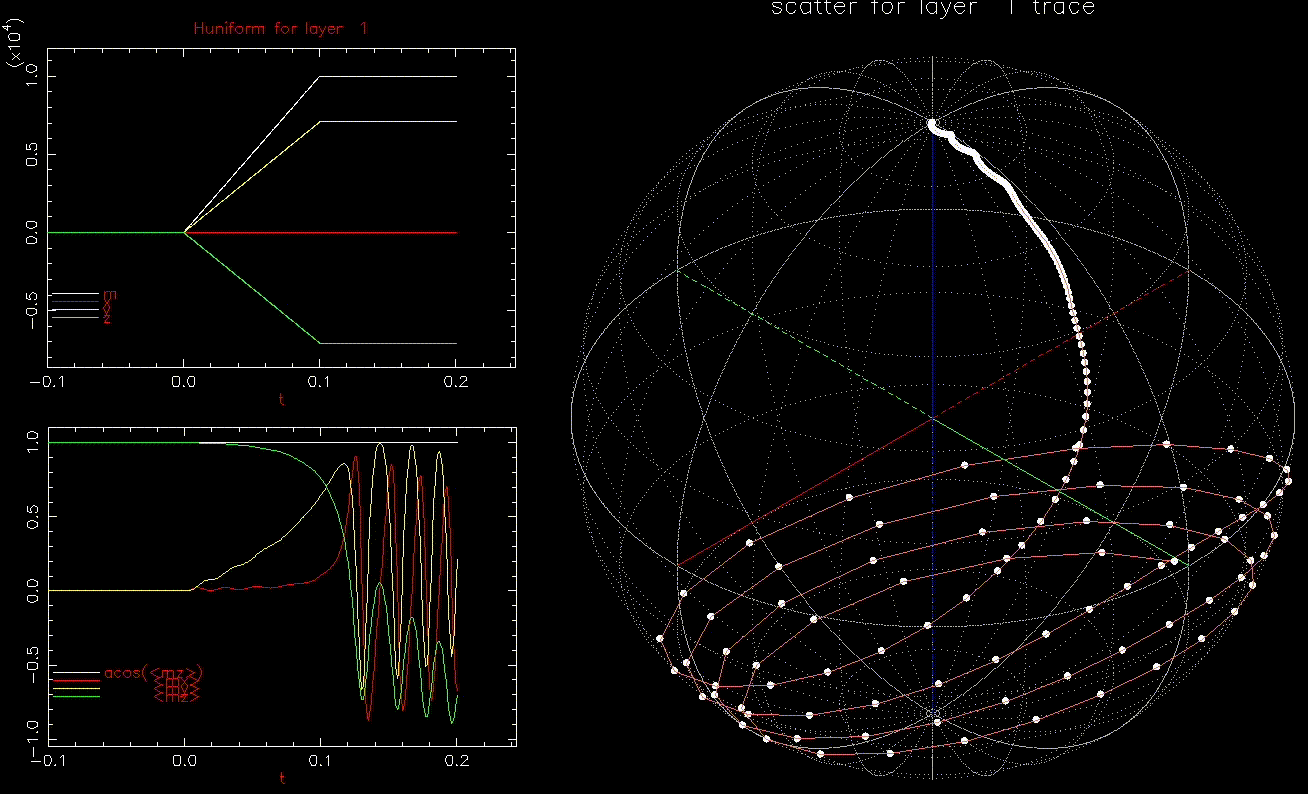
 as a function of time (ns), white, red, yellow, green are magnitude, x, y, z components, respectively; right: isometric projection of unit sphere, dot represent the orientation of one of the 1024 grains updated every 1ps with line connecting to previous orientation.
as a function of time (ns), white, red, yellow, green are magnitude, x, y, z components, respectively; right: isometric projection of unit sphere, dot represent the orientation of one of the 1024 grains updated every 1ps with line connecting to previous orientation.  is ramped from 0 to 10kOe in 0.1ns.
is ramped from 0 to 10kOe in 0.1ns.As expected, all 1024 grains behave identically and are nearly in equilbrium with ![]() until switching. Damping will limit how quickly
until switching. Damping will limit how quickly ![]() can be reversed.
can be reversed.
We next look at dynamic writing by ![]() where
where ![]() the average of
the average of ![]() over the 1024 grains at time t.
over the 1024 grains at time t.
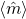 as a function of time (ns), white, red, yellow, green are magnitude, x, y, z components, respectively; right: isometric projection of unit sphere, dot represent the orientation of one of the 1024 grains updated every 1ps with line connecting to previous orientation.
as a function of time (ns), white, red, yellow, green are magnitude, x, y, z components, respectively; right: isometric projection of unit sphere, dot represent the orientation of one of the 1024 grains updated every 1ps with line connecting to previous orientation. 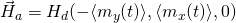 is ramped from 0 to 1.5kOe in 0.1ns.
is ramped from 0 to 1.5kOe in 0.1ns.This is an interesting result, we can switch a grain with ![]() in less than 0.2ns. In fact, as long as
in less than 0.2ns. In fact, as long as ![]() , the grain will switch, albeit with longer required time. Increasing
, the grain will switch, albeit with longer required time. Increasing ![]() reduces the time to switch.
reduces the time to switch.
Finally, let us apply a conventional write field and then include an dynamic field to assist in writing. Here, ![]() .
.
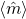 as a function of time (ns), white, red, yellow, green are magnitude, x, y, z components, respectively; right: isometric projection of unit sphere, dot represent the orientation of one of the 1024 grains updated every 1ps with line connecting to previous orientation.
as a function of time (ns), white, red, yellow, green are magnitude, x, y, z components, respectively; right: isometric projection of unit sphere, dot represent the orientation of one of the 1024 grains updated every 1ps with line connecting to previous orientation. 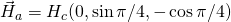 is ramped from 0 to 6kOe in 0.1ns and held then
is ramped from 0 to 6kOe in 0.1ns and held then 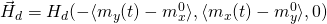 is ramped from 0 to 1.5kOe in 0.1ns and added to
is ramped from 0 to 1.5kOe in 0.1ns and added to 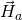 .
.In this case, even ![]() of 300 Oe can still switch the grain, albeit in ~0.4ns:
of 300 Oe can still switch the grain, albeit in ~0.4ns:

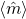 as a function of time (ns), white, red, yellow, green are magnitude, x, y, z components, respectively; right: isometric projection of unit sphere, dot represent the orientation of one of the 1024 grains updated every 1ps with line connecting to previous orientation.
as a function of time (ns), white, red, yellow, green are magnitude, x, y, z components, respectively; right: isometric projection of unit sphere, dot represent the orientation of one of the 1024 grains updated every 1ps with line connecting to previous orientation. 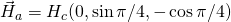 is ramped from 0 to 6kOe in 0.1ns and held then
is ramped from 0 to 6kOe in 0.1ns and held then 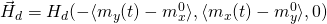 is ramped from 0 to 300 Oe in 0.1ns and added to
is ramped from 0 to 300 Oe in 0.1ns and added to 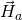 .
.This latter case is similar to microwave assisted magnetic recording (MAMR). Here, instead of having a time varying ![]() it is a fixed frequency of about ~
it is a fixed frequency of about ~![]() GHz/kOe
GHz/kOe ![]() and
and ![]() large to reduce the number of required cycles.
large to reduce the number of required cycles.
While the simulation correctly follows the governing physics, we have not simulated an realizable physical device. While identical square prism grains are not realistic, they are not impossible.
No, we have made at least two mistakes. First, since the grains are identical including their initial orientations we have introduce a high degree of symmetry into the problem. In fact this is clearly shown in the results. Each simulation has 1024 grains, but only one phase space point appears. That is, all 1024 grains have identical trajectories. This happened due to our second mistake.
LLG includes damping. This damping is energy exchange between the magnetic system and the lattice it finds itself in. Since the magnetic grains are small, there are not insignificant thermal fluctuations in the magnetization orientation due to the lattice[1]. This effect needs to be included for realistic simulation of actual physical devices.
The result of thermal fluctuations is to introduce a variation of ![]() around the equilibrium orientation. In conventional recording this introduces a diffusive flux which allows some grains to switch even when
around the equilibrium orientation. In conventional recording this introduces a diffusive flux which allows some grains to switch even when ![]() . In dynamic recording,
. In dynamic recording, ![]() has a distribution in
has a distribution in ![]() and
and ![]() causing either a mismatched phase or distribution of resonant angular frequency
causing either a mismatched phase or distribution of resonant angular frequency ![]() , respectively. And, of course, it breaks the high symmetry of the results reported here.
, respectively. And, of course, it breaks the high symmetry of the results reported here.

[…] previous posts, we discussed magnetic recording. Here, we extend this discussion by looking at the effect of […]
[…] the previous posts on magnetic recording, we are now in the position to look at unconventional magnetic […]