In a previous post, we discussed magnetic recording. Here, we extend this discussion by looking at the effect of magnetostatic fields during recording.
It is well known that magnetostatic interactions between magnetic grains can affect the probability of writing (or flipping) a grain. The best known example of this is ‘non-linear transition shift (NLTS)’ which causes a shift of the ‘transition’ between a group of grains written in one orientation followed by another group of grains written in a different orientation. For perpendicular medium (all currently shipping HDD), this interaction tries to pull the transition towards the first group. Depending on the size of this shift, this can degrade the performance of a recording system. Typically, by slightly adjusting the coil current timing in the write head, the effect can be minimized.
Another effect of the magnetostatic field during magnetic recording is the coupling of otherwise independent grains. Through the interaction of the magnetostatic field, energy can be shared between two (or more) grains. This sharing can cause correlations between the dynamics of the magnetic moments in otherwise independent grains.
The magnetostatic field due from an uniform magnetized volume ![]() with surface area
with surface area ![]() (and volume
(and volume ![]() ) is
) is
![]()
where ![]() and
and ![]() is the outward direction normal of area
is the outward direction normal of area ![]() . In micro-magnetics, we are concerned with volume averaged fields over volumes of uniformed magnetization
. In micro-magnetics, we are concerned with volume averaged fields over volumes of uniformed magnetization
(1) 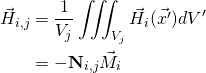
would be the magnetostatic field on ![]() due to
due to ![]() and
and ![]() is a 3×3 matrix. The total field acting on
is a 3×3 matrix. The total field acting on ![]() is
is
(2) 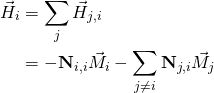
where we have arbitrarily split the field in to a ‘self demagnetizing’ and magnetostatic field from other moments. For rectangular prisms or ellipsoids, ![]() is diagonal with trace of
is diagonal with trace of ![]() (1 in S.I.). For square prisms or cylinders (extruded in
(1 in S.I.). For square prisms or cylinders (extruded in ![]() ), the free energy is
), the free energy is
(3) ![Rendered by QuickLaTeX.com \begin{align*} $$G_{i,\mathbf{N}}&=\frac{M_{s_i}^2}{2}\hat{m}_i \cdot \mathbf{N}_{i,i} \hat{m}_i \\ &=\frac{M_{s_i}^2}{2} \left[ m_{x_i}^2 (2\pi - N/2) + m_{y_i}^2 (2\pi -N/2) + m_{z_i}^2 N \right] \\ &=(3 N / 4 - \pi)M_{s_i}^2 m_{z_i}^2 \end{align*}](https://entonos.com/wp-content/ql-cache/quicklatex.com-3e7d5d7991934bc89b8cb2f1ef081f27_l3.png)
where we have ignored an irrelevant constant in the free energy and ![]() is the
is the ![]() element of the diagonal
element of the diagonal ![]() . If the magnetocrystalline anisotropy (MCA) also has its ‘easy axis’ along
. If the magnetocrystalline anisotropy (MCA) also has its ‘easy axis’ along ![]() , then its energy is
, then its energy is ![]() has a similar functional form and they can be combined to give
has a similar functional form and they can be combined to give ![]() . If
. If ![]() (a value for a sphere), then the self demagnetizing field enhances the effective MCA, otherwise it decreases it. That is, tall grains have an increased MCA while short grains have a reduced MCA- the so-called ‘shape anisotropy’. In terms of
(a value for a sphere), then the self demagnetizing field enhances the effective MCA, otherwise it decreases it. That is, tall grains have an increased MCA while short grains have a reduced MCA- the so-called ‘shape anisotropy’. In terms of ![]() .
.
For less symmetric extruded shapes, ![]() simply becomes symmetric and one new
simply becomes symmetric and one new ![]() element is non-zero.
element is non-zero.
To see the effects of the magnetostatic fields on the dynamics of the magnetic moments, we will compare the results of micro-magnetic simulations with no magnetostatic fields, only ‘self demagnetizing’ fields and full magnetostatic fields. Only in the later case would the collection of grains be coupled.
For micro-magnetic simulations, we have 1024 identical square prism (extruded 10nm) grains of volume 503nm![]() packed in a periodic square lattice with
packed in a periodic square lattice with ![]() kOe,
kOe, ![]() (
(![]() ) is normal to media plane,
) is normal to media plane, ![]() emu/cc and
emu/cc and ![]() . We start with all the grains along
. We start with all the grains along ![]() (or
(or ![]() for ‘random’ initial orientation) and apply an uniform field of
for ‘random’ initial orientation) and apply an uniform field of ![]() slowly ramping
slowly ramping ![]() from zero to
from zero to ![]() in 5ns.
in 5ns.
| magnetostatic field | packing fraction (%) | initial orientation | |||
| none | 83 or 100 | up or random | 14.0 | 14.0 | 0 |
| self demagnetization | 83 or 100 | up or random | 14.5 | 14.5 | 0 |
| full | 100 | up | 9.6 | 9.6 | 0 |
| full | 100 | random | 11.6 | 18.0 | 6.4 |
| full | 83 | up | 9.7 | 17.8 | 8.1 |
| full | 83 | random | 11.8 | 17.8 | 6.0 |
For the both no magnetostatic and self demagnetizing cases, all of the magnetic moments are identical and independent, therefore not surprising they both satisfy the Stoner-Wohlfarth limit (![]() ). Of course for the self demagnetization case, the effective
). Of course for the self demagnetization case, the effective ![]() is
is ![]() kOe (i.e.
kOe (i.e. ![]() here). Similarly, for the full magnetostatic case with 100% packing,
here). Similarly, for the full magnetostatic case with 100% packing, ![]() kOe. Since the grains are identical, start with the same initial condition, have the same applied field and are arranged in a periodic lattice, it is equivalent of having an uniform infinite thin layer of magnetization (i.e.
kOe. Since the grains are identical, start with the same initial condition, have the same applied field and are arranged in a periodic lattice, it is equivalent of having an uniform infinite thin layer of magnetization (i.e. ![]() ).
).
Once the symmetry of the full magnetostatic case is broken (83% packing fraction or random initial orientations), we first observe that the required ![]() to either flip the first grain or flip all grains are not the same. Here the required field to flip all the grains is relatively constant while the field to flip the first grain depends mostly on the initial orientations- random orientation requiring a larger field. In other words, even though identical grains are used, symmetry breaking leads to a ‘switching field distribution’. This demonstrates that the magnetostatic field can couple grains and affect their dynamic behavior.
to either flip the first grain or flip all grains are not the same. Here the required field to flip all the grains is relatively constant while the field to flip the first grain depends mostly on the initial orientations- random orientation requiring a larger field. In other words, even though identical grains are used, symmetry breaking leads to a ‘switching field distribution’. This demonstrates that the magnetostatic field can couple grains and affect their dynamic behavior.
Clearly, square prism grains is a simplification. Instead one could group small square prisms into granular type microstucture that can reasonably approximate experimental results. Here we used a periodic 256 ![]() 256 square prism array to construct 481 grains. For comparison, we also display the square prism grains at 83% packing.
256 square prism array to construct 481 grains. For comparison, we also display the square prism grains at 83% packing.
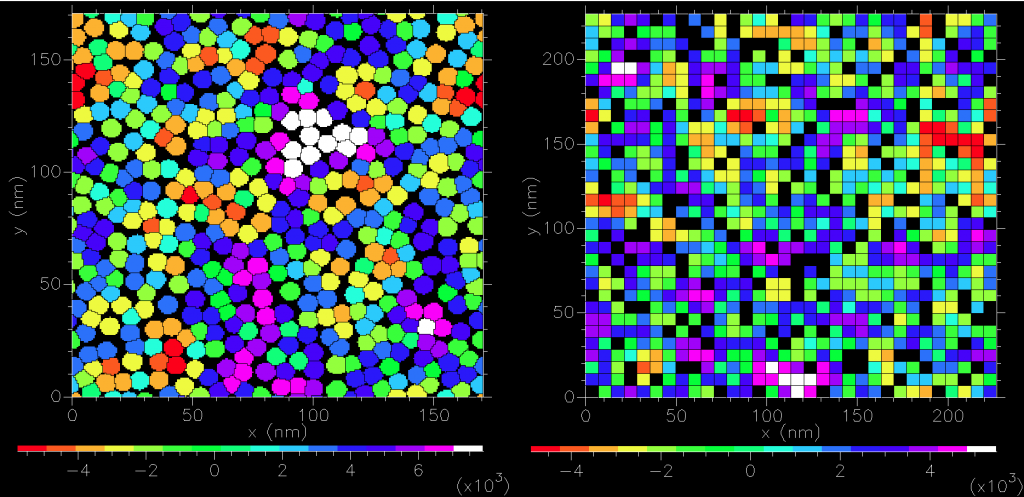
 ) and 83% packing fraction (black is void or grain boundaries). Left is 481 grains with mean diameter 8nm and standard deviation of 0.4nm. Right is 849 square prisms grains.
) and 83% packing fraction (black is void or grain boundaries). Left is 481 grains with mean diameter 8nm and standard deviation of 0.4nm. Right is 849 square prisms grains.| magnetostatic field | initial orientation | |||
| none | up or random | 14.0 | 14.0 | 0 |
| self demagnetization | up or random | 14.2 | 14.8 | 0.6 |
| full | up | 9.9 | 17.8 | 7.9 |
| full | random | 11.9 | 17.9 | 6.0 |
It should not be surprising that the no magnetostatic case does not change between realistic microstructure compared to square prism grains. In both cases, the energy and effective fields are the same. For the self demagnetization case, we see a slight reduction of ![]() for the first grain to flip and a slight increase for all grains to flip. Both can be contributed to the fact
for the first grain to flip and a slight increase for all grains to flip. Both can be contributed to the fact ![]() is not diagonal but has a non-zero
is not diagonal but has a non-zero ![]() component. Similar effect can be see for the full magnetostatic field case.
component. Similar effect can be see for the full magnetostatic field case.
The point is that for physically reasonable results, a full magnetostatic calculation is necessary since the coupling between grains does affect the dynamics of any particular grain, even in the case where the applied field is slowly varying. Such effects are magnified for faster varying applied fields. Be wary of simulations of magnetic recording that do not include the full magnetostatic field calculation (there are many), they will lead you astray.

[…] previous posts, we discussed magnetic recording. Here, we extend this discussion by looking at the effect of a […]
[…] is the depolarization (or demagnetization) factor along ranging from (a needle) to (pancake) [see]. If not in isolation, other grains would contribute to , as a summation of dipole fields in the […]
[…] the previous posts on magnetic recording, we are now in the position to look at unconventional magnetic recording. In […]