magnetostatics in magnetic recording

In a previous post, we discussed magnetic recording. Here, we extend this discussion by looking at the effect of magnetostatic fields during recording.

It is well known that magnetostatic interactions between magnetic grains can affect the probability of writing (or flipping) a grain. The best known example of this is ‘non-linear transition shift (NLTS)’ which causes a shift of the ‘transition’ between a group of grains written in one orientation followed by another group of grains written in a different orientation. For perpendicular medium (all currently shipping HDD), this interaction tries to pull the transition towards the first group. Depending on the size of this shift, this can degrade the performance of a recording system. Typically, by slightly adjusting the coil current timing in the write head, the effect can be minimized.

Another effect of the magnetostatic field during magnetic recording is the coupling of otherwise independent grains. Through the interaction of the magnetostatic field, energy can be shared between two (or more) grains. This sharing can cause correlations between the dynamics of the magnetic moments in otherwise independent grains.

The magnetostatic field due from an uniform magnetized volume $\vec{M}_i = M_{s_i} \hat{m}_i$ with surface area $S_i$ (and volume $V_i$ ) is

$\vec{H}_i(\vec{x}) = - \nabla \oint_{S_i} \frac{\sigma_i(\vec{x'}) da'}{|\vec{x}-\vec{x'}|}$

where $\sigma_i(\vec{x})=\hat{n} \cdot \vec{M}_i$ and $\hat{n}$ is the outward direction normal of area $da$ . In micro-magnetics, we are concerned with volume averaged fields over volumes of uniformed magnetization

(1) $\begin{align*} $$\vec{H}_{i,j} &=\frac{1}{V_j} \iiint_{V_j} \vec{H}_i(\vec{x'}) dV' \\&= -\mathbf{N}_{i,j} \vec{M}_i \end{align*}$

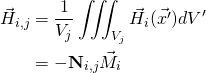
would be the magnetostatic field on $\vec{M}_j$ due to $\vec{M}_i$ and $\mathbf{N}_{i,j}$ is a 3×3 matrix. The total field acting on $\vec{M}_i$ is

(2) $\begin{align*} $$\vec{H}_i &=\sum_j \vec{H}_{j,i} \\&= - \mathbf{N}_{i,i} \vec{M}_i - \sum_{j \neq i} \mathbf{N}_{j,i} \vec{M}_j \end{align*}$

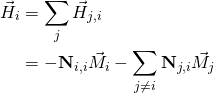
where we have arbitrarily split the field in to a ‘self demagnetizing’ and magnetostatic field from other moments. For rectangular prisms or ellipsoids, $\mathbf{N}_{i,i}$ is diagonal with trace of $4\pi$ (1 in S.I.). For square prisms or cylinders (extruded in $z$ ), the free energy is

(3) $\begin{align*} $$G_{i,\mathbf{N}}&=\frac{M_{s_i}^2}{2}\hat{m}_i \cdot \mathbf{N}_{i,i} \hat{m}_i \\ &=\frac{M_{s_i}^2}{2} \left[ m_{x_i}^2 (2\pi - N/2) + m_{y_i}^2 (2\pi -N/2) + m_{z_i}^2 N \right] \\ &=(3 N / 4 - \pi)M_{s_i}^2 m_{z_i}^2 \end{align*}$

where we have ignored an irrelevant constant in the free energy and $N$ is the $z$ element of the diagonal $\mathbf{N}_{i,i}$ . If the magnetocrystalline anisotropy (MCA) also has its ‘easy axis’ along $\hat{z}$ , then its energy is $- H_k M_{s_i} m_{z_i}^2/2$ has a similar functional form and they can be combined to give $\left[(3 N / 4 - \pi) M_{s_i} - H_k / 2\right] M_{s_i} m_{z_i}^2$ . If $N < 4 \pi /3$ (a value for a sphere), then the self demagnetizing field enhances the effective MCA, otherwise it decreases it. That is, tall grains have an increased MCA while short grains have a reduced MCA- the so-called ‘shape anisotropy’. In terms of $\vec{H}_k = - \nabla_{\vec{M}_i} G = \left[H_k - (3 N /2 - 2\pi)M_{s_i}\right] m_{z_i} \hat{z}$ .

For less symmetric extruded shapes, $\mathbf{N}_{i,i}$ simply becomes symmetric and one new $xy$ element is non-zero.

To see the effects of the magnetostatic fields on the dynamics of the magnetic moments, we will compare the results of micro-magnetic simulations with no magnetostatic fields, only ‘self demagnetizing’ fields and full magnetostatic fields. Only in the later case would the collection of grains be coupled.

For micro-magnetic simulations, we have 1024 identical square prism (extruded 10nm) grains of volume 503nm $^3$ packed in a periodic square lattice with $H_k=28$ kOe, $\hat{z}$ ( $=\hat{k}$ ) is normal to media plane, $M_s=700$ emu/cc and $\alpha=0.02$ . We start with all the grains along $\hat{z}$ (or $\pm \hat{z}$ for ‘random’ initial orientation) and apply an uniform field of $\vec{H}_a = H_a(0,\sin \pi/4,-\cos\pi/4)$ slowly ramping $H_a$ from zero to $H_a$ in 5ns.

magnetostatic field	packing fraction (%)	initial orientation	$H_a$ to flip at least one (kOe)	$H_a$ to flip all (kOe)	$\Delta H_a$ (kOe)
none	83 or 100	up or random	14.0	14.0	0
self demagnetization	83 or 100	up or random	14.5	14.5	0
full	100	up	9.6	9.6	0
full	100	random	11.6	18.0	6.4
full	83	up	9.7	17.8	8.1
full	83	random	11.8	17.8	6.0

Table 1: Required $\vec{H}_a = H_a (0, \sin \pi/4, -\cos \pi/4)$ to flip first or all grains for square prisms grains (10nm height and volume 503nm^3) on a square periodic lattice.

For the both no magnetostatic and self demagnetizing cases, all of the magnetic moments are identical and independent, therefore not surprising they both satisfy the Stoner-Wohlfarth limit ( $H_a \rightarrow H_k/2$ ). Of course for the self demagnetization case, the effective $H_k$ is $\left[H_k -(3 \times 3.2811/2 - 2\pi) M_s\right] = 29$ kOe (i.e. $N=3.2811$ here). Similarly, for the full magnetostatic case with 100% packing, $H_a = (H_k -4\pi M_s)/2=9.6$ kOe. Since the grains are identical, start with the same initial condition, have the same applied field and are arranged in a periodic lattice, it is equivalent of having an uniform infinite thin layer of magnetization (i.e. $N=4\pi$ ).

Once the symmetry of the full magnetostatic case is broken (83% packing fraction or random initial orientations), we first observe that the required $H_a$ to either flip the first grain or flip all grains are not the same. Here the required field to flip all the grains is relatively constant while the field to flip the first grain depends mostly on the initial orientations- random orientation requiring a larger field. In other words, even though identical grains are used, symmetry breaking leads to a ‘switching field distribution’. This demonstrates that the magnetostatic field can couple grains and affect their dynamic behavior.

Clearly, square prism grains is a simplification. Instead one could group small square prisms into granular type microstucture that can reasonably approximate experimental results. Here we used a periodic 256 $\times$ 256 square prism array to construct 481 grains. For comparison, we also display the square prism grains at 83% packing.

Full magnetostatic field (Oe) for each grain- 10nm tall, randomly orientated (i.e. $\hat{m}\cdot\hat{k}=\pm 1$ ) and 83% packing fraction (black is void or grain boundaries). Left is 481 grains with mean diameter 8nm and standard deviation of 0.4nm. Right is 849 square prisms grains.

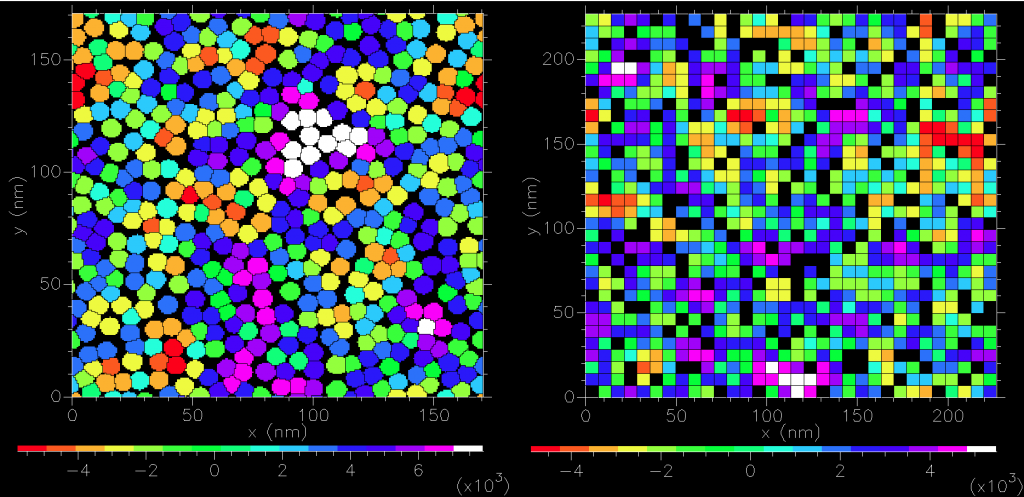
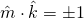Full magnetostatic field (Oe) for each grain- 10nm tall, randomly orientated (i.e. $\hat{m}\cdot\hat{k}=\pm 1$ ) and 83% packing fraction (black is void or grain boundaries). Left is 481 grains with mean diameter 8nm and standard deviation of 0.4nm. Right is 849 square prisms grains.

magnetostatic field	initial orientation	$H_a$ to flip at least one (kOe)	$H_a$ to flip all (kOe)	$\Delta H_a$ (kOe)
none	up or random	14.0	14.0	0
self demagnetization	up or random	14.2	14.8	0.6
full	up	9.9	17.8	7.9
full	random	11.9	17.9	6.0

Table 2: Required $\vec{H}_a = H_a (0, \sin \pi/4, -\cos \pi/4)$ to flip first or all grains with mean diameter of 8nm and standard deviation of 0.4nm (10nm height) on a periodic lattice.

It should not be surprising that the no magnetostatic case does not change between realistic microstructure compared to square prism grains. In both cases, the energy and effective fields are the same. For the self demagnetization case, we see a slight reduction of $H_a$ for the first grain to flip and a slight increase for all grains to flip. Both can be contributed to the fact $\mathbf{N}_{i,i}$ is not diagonal but has a non-zero $xy$ component. Similar effect can be see for the full magnetostatic field case.

The point is that for physically reasonable results, a full magnetostatic calculation is necessary since the coupling between grains does affect the dynamics of any particular grain, even in the case where the applied field is slowly varying. Such effects are magnified for faster varying applied fields. Be wary of simulations of magnetic recording that do not include the full magnetostatic field calculation (there are many), they will lead you astray.

3 Responses

stochastic effects in magnetic recording – Entonos June 30, 2020 at 2:10 pm

[…] previous posts, we discussed magnetic recording. Here, we extend this discussion by looking at the effect of a […]

introduction to magnetic recording – Entonos June 30, 2020 at 8:02 pm

[…] is the depolarization (or demagnetization) factor along ranging from (a needle) to (pancake) [see]. If not in isolation, other grains would contribute to , as a summation of dipole fields in the […]

unconventional magnetic recording – Entonos July 30, 2020 at 4:03 pm

[…] the previous posts on magnetic recording, we are now in the position to look at unconventional magnetic recording. In […]

3 Responses

Add a Comment Cancel reply